Week 1: Closure#
Key Concepts#
Scalar functions: particularly quadratic forms
Vector functions
Visualization of functions: Graphs and level curves/sets
Continuity
The standard inner product (dot product) and norm in \(\mathbb{R}^n\)
Partial derivatives and the Gradient vector
If there are still concepts you are unsure about, you should reread the relevant chapters in the textbook.
Extra Exercises#
First, complete exercises from the preparation and Long and Short Day that you have not yet finished.
1: Visualizations - A Hike on a Mountain#
We are looking at a topographic map of a mountain, where the circles represent the level curves of the elevation function. The arrows indicate the gradient vector field of the elevation function. On the mountain, there is an elliptical hiking trail, which is marked in red on the map.
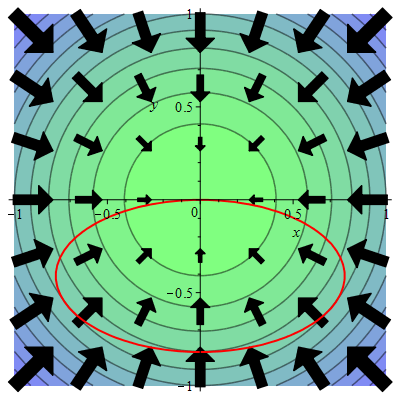
Question a#
Imagine that you are walking along the red hiking trail counterclockwise as seen from above. Find the points on the trail where the slope is 0 (neither uphill nor downhill).
Hint
There are four such points.
Answer
On a level curve, the elevation does not change. Therefore, you need to find the points on the trail where the trail shares a tangent with a level curve.
Question b#
On which parts of the trail are you walking uphill, and on which are you walking downhill?
Question c#
Follow one of the level curves on the map all the way around and observe the direction of the gradient vectors nearby. Conclusion?
Question d#
This mountain is, of course, quite special. But put on your hiking boots again and provide an intuitive argument for why gradient vectors must always, on all mountains, be perpendicular to the level curves.
Answer
Suggestion: If we think of the level curve as a path we are walking along, then the journey is effortless. We are walking horizontally - neither uphill nor downhill - the entire time. It seems natural that the slope would be greatest if we suddenly changed direction by 90 degrees upward. Agree?
2: Continuity of First-Degree Polynomials#
Prove that the polynomial function \(f : \mathbb{R} \to \mathbb{R}\), \(f(x) = 3x\) is continuous at all points \(x \in \mathbb{R}\).
Hint
Use the \(\epsilon-\delta\) definition. See this equation in the textbook.
Hint
Let \(x_0\) be an arbitrary real number, and let \(\epsilon > 0\) be given. You now need to specify how to choose \(\delta > 0\) (it may depend on \(x_0\) and \(\epsilon\)) such that \(|x - x_0| < \delta \Rightarrow |f(x) - f(x_0)| < \epsilon\).

