Demo 1: Continuity, Plotting, and Partial Derivatives

Demo by Christian Mikkelstrup, Hans Henrik Hermansen, Jakob Lemvig, Karl Johan Måstrup Kristensen and Magnus Troen

from sympy import *
from dtumathtools import *
init_printing()

Welcome back after Christmas and January, and welcome to spring in Math1. There will be a whole lot of new curriculum, and among other things a whole lot of 3D plots! For this we have developed the Python library dtumathtools, which will accompany you during the spring. It contains dtuplot which should be used for plotting, as well as several good helper functions. You should have dtumathtools installed from Math1a; if not, please run the command

pip install -U dtumathtools 

in your terminal.

Functions (of One Variable)

We can define the function \(f: \mathbb{R} \to \mathbb{R}\), \(f(x)=x \operatorname{e}^x\) as a python function using the familiar command:

def f(x):  
    return x * exp(x)

The function is evaluated at the point \(x = -2\) with the command:

f(-2)

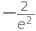
Which has the numerical value:

f(-2).evalf()

It is, however, rarely necessary to define functions with the def command, and we will often work directly with the function expression:

x = symbols('x', real = True)          # Necessary to use x as a symbolic variable (note the real=True, since R -> R)
f_expr = x * exp(x)
f_expr

Which is evaluated by:

f_expr.subs(x, -2)

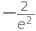
The function can be differentiated by:

f_prime = f_expr.diff(x)
f_prime

We can also investigate the limits for \(x \to -\infty\), \(x \to \infty\) and \(x \to -2\) with the commands:

f_expr.limit(x, -oo), f_expr.limit(x, oo), f_expr.limit(x, -2)

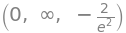
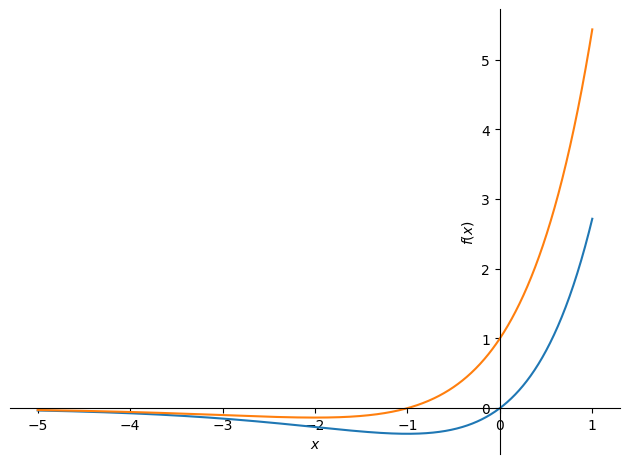
It should be no surprise that \(\lim_{x \to -2} f(x) = f(-2)\), since the function is continuous everywhere.

We can plot the function and its derivative by:

plot(f_expr, f_prime, (x, -5, 1))

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7f1888900c70>

A little more complicated example could be the piecewise-defined function \(g: \mathbb{R} \to \mathbb{R}\):

\[\begin{equation*} g(x) = \begin{cases} -x & x <0 \\ \operatorname{e}^x & x \ge 0 \end{cases}\,\,, \end{equation*}\]

which in Python would be defined by:

def g(x):
    if x < 0:
        return -x
    else:
        return exp(x)

Using Sympy, we can define it as follows:

g_expr = Piecewise((-x, x < 0), (exp(x), x >= 0))
g_expr

\[\begin{split}\displaystyle \begin{cases} - x & \text{for}\: x < 0 \\e^{x} & \text{otherwise} \end{cases}\end{split}\]

which evaluates as expected:

g_expr.subs(x, -2)

We plot it using:

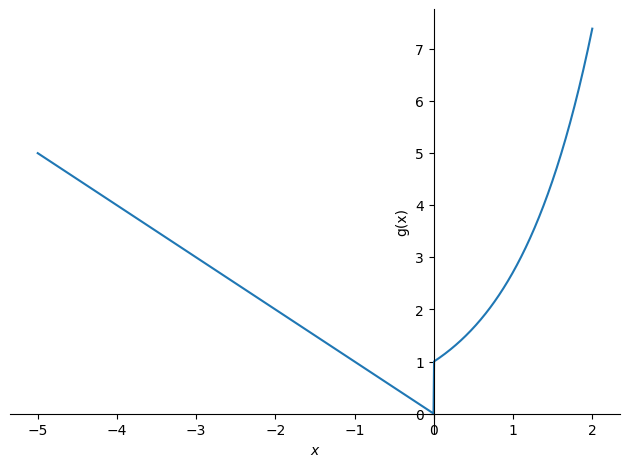
plot(g_expr,(x,-5,2), ylabel='g(x)')

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7f1869b2f8e0>

Notice that the function is discontinuous at \(x = 0\). Be aware that Python/CAS cannot be used to prove discontinuity at \(x = 0\). This would require a so called epsilon-delta-argument, which Python/CAS cannot help us with. Sympy will, for example, differentiate the function without raising any suspicion of discontinuity.

g_expr.diff(x)

\[\begin{split}\displaystyle \begin{cases} -1 & \text{for}\: x < 0 \\e^{x} & \text{otherwise} \end{cases}\end{split}\]

We should, however, note that the function isn’t differentiable at \(x = 0\), since it isn’t continuous at this point.

Partial Derivatives using diff

For functions of multiple variables we will introduce the partial derivative, as well as how they can be used. To showcase the partial derivatives we will consider the function:

x, y = symbols('x y')
f = x*y**2+x
f

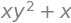
which can be differentiated using diff:

f.diff(x), f.diff(y)

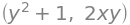
Each of these expressions can be differentiated with respect to \(x\) and \(y\). Doing that would yield the following four functions:

f.diff(x).diff(x), f.diff(x).diff(y), f.diff(y).diff(x), f.diff(y).diff(y)

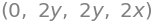
These are the second-order derivatives, and they can be calculated quicker as follows:

f.diff(x,2), f.diff(y,2), f.diff(x,y), f.diff(y,x)

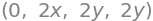
We can substitute in values for \(x\) and \(y\) and calculate, for example, \(\frac{\partial}{\partial x}f(x,y)\) evaluated at \((-2,3)\):

f.diff(x).subs({x:-2,y:3})

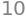
or \(\frac{\partial}{\partial x\partial y}f(x,y)\), evaluated at \((5,-13)\):

f.diff(x,y).subs({x:5,y:-13})

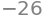
Plots

Orienting Graphs

We will now consider functions of multiple variables, hence plotting in 3D! This leaves us a decision to make, since we need to choose which angle we want to see the graphs from. If we don’t do anything dtuplot, will choose an angle for us, but if we wish to inspect the graph from a certain angle, then camera can be used. Try changing the values for elev and azim.

f = 4-x**2-y**2

p=dtuplot.plot3d(f, (x,-3,3),(y,-3,3), camera = {"elev": 25, "azim": 45})

The plot above was generated as a static PNG-file, which is great if you wish to print or export the Notebook as a PDF. All plots will be static if we don’t do anything or if we use the command %matplotlib inline.

If we instead run the command %matplotlib qt (which in the following block has been commented out; try running the block after removing #), then we enable interactive plots. All subsequent plots, will now “pop out” of VS Code, where we now can rotate the graph.

# %matplotlib qt

About Interactive Plots

Note: %matplotlib qt only works when running python on your own computer. It will, for instance, not work if you run Python on an online server like Google Colab. In such cases, widgets can be used instead %matplotlib ipympl. This does, however, require you to install the package ipympl.

Overview of commands:

# %matplotlib inline        # static plots
# %matplotlib qt            # QT (cute) interactive pop-out plots
# %matplotlib ipympl        # Widget/ipynpl interactive inline plots (not as stable as QT, may require a restart of the kernel)
# %matplotlib --list        # list of all backends

Aesthetics

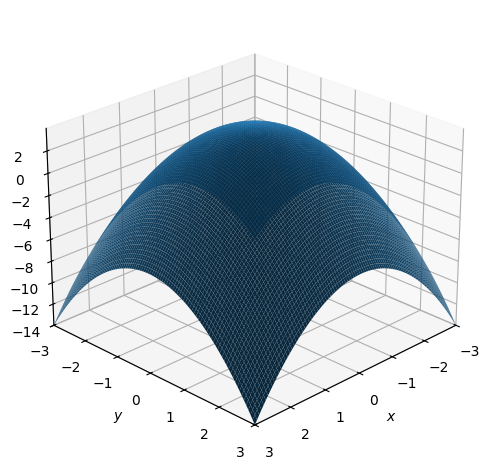
When we wish to change the aesthetics of our plots, we’ll need to use rendering_kw={...} which may look intimidating. It just tells which rendering settings to use, for example color, alpha etc. In most cases it’s adequate to just write {...}, which dtuplot will know means aesthetics.

dtuplot.plot3d(f, (x,-3,3),(y,-3,3), wireframe = True, rendering_kw = {"color": "red", "alpha": 0.5})

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f1868ae0700>

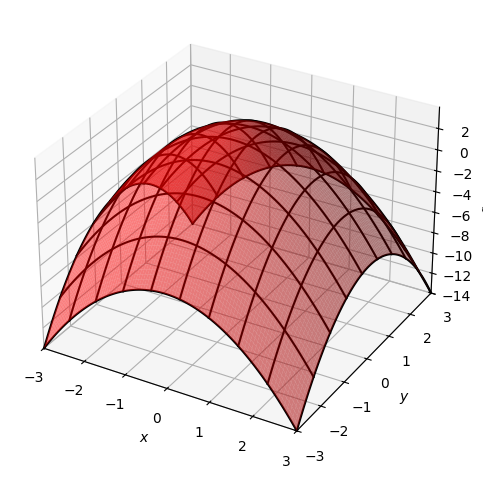
Some aesthetic choices are special enough to be outside of rendering_kw, for example wireframe as seen above, or use_cm which denotes each value with a color, as seen below.

p=dtuplot.plot3d(f, (x,-3,3),(y,-3,3), use_cm=True, legend=True)

Contours

We can also plot contours, i.e. a 2D plot of a 3D structure by:

dtuplot.plot_contour(f, (x,-3,3),(y,-3,3), is_filled=False)

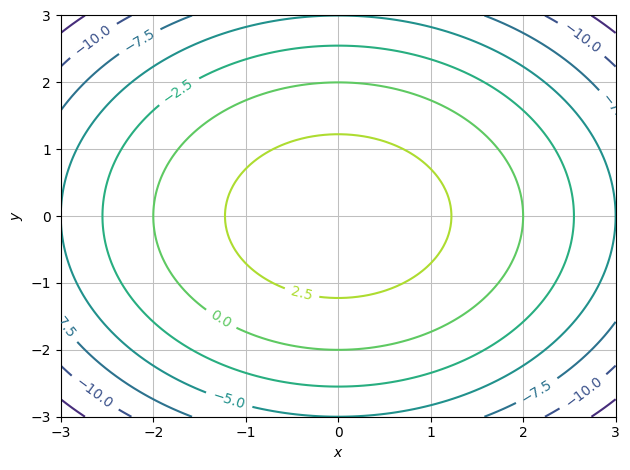
<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f18695a8fd0>

And if we wish to choose the exact values shown:

zvals = [-2,-1,0,1]
dtuplot.plot_contour(f, (x,-3,3),(y,-3,3), rendering_kw={"levels":zvals, "alpha":0.5}, is_filled=False)

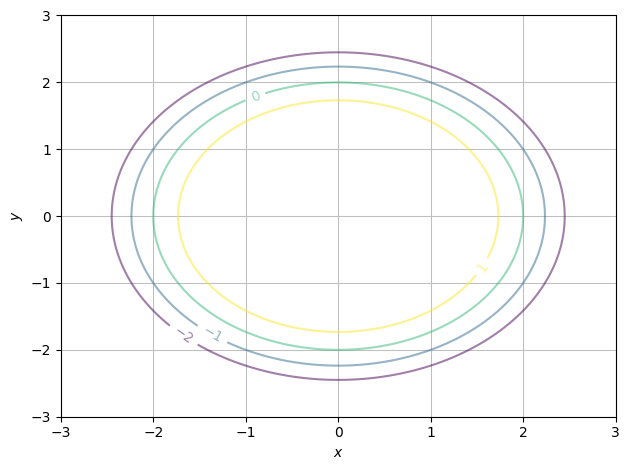
<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f18626e94c0>

Gradient Vector Fields

Consider the vector field

(5)\[\begin{equation} f(x,y)=\cos(x)+\sin(y). \end{equation}\]

The gradient of \(f\) can be computed as:

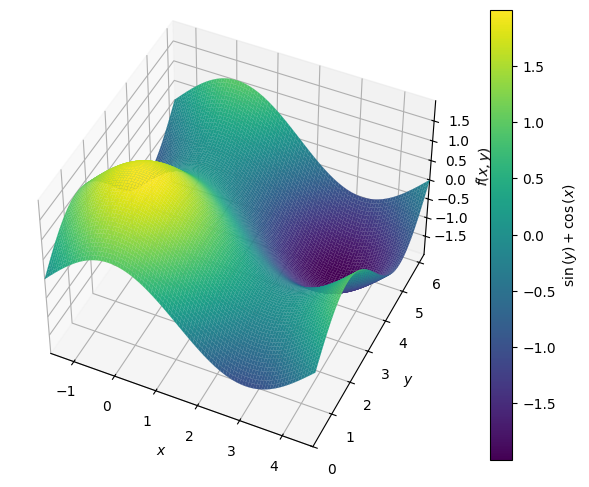
f = cos(x)+sin(y)
nf = Matrix([f.diff(x), f.diff(y)])
nf

\[\begin{split}\displaystyle \left[\begin{matrix}- \sin{\left(x \right)}\\\cos{\left(y \right)}\end{matrix}\right]\end{split}\]

The gradient can also be computed using dtutools.gradient. Note that this function doesn’t tell us in which order the variables are differentiated.

dtutools.gradient(f)

\[\begin{split}\displaystyle \left[\begin{matrix}- \sin{\left(x \right)}\\\cos{\left(y \right)}\end{matrix}\right]\end{split}\]

The gradient vector field can be plotted as shown:

dtuplot.plot_vector(nf, (x,-pi/2,3/2*pi),(y,0,2*pi),scalar=False)

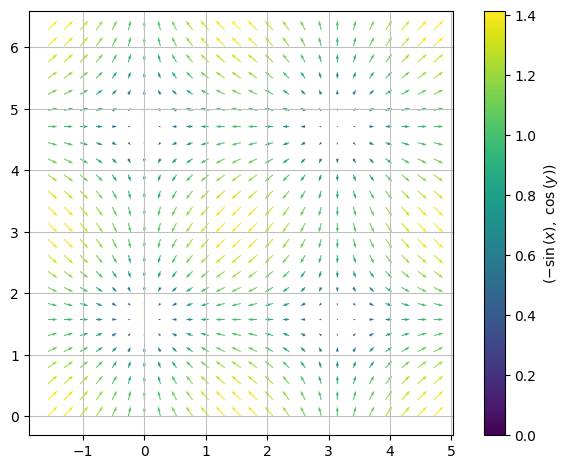
<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f1861f62760>

Or if we want to get fancy (note that rendering_kw has been split, such that the arrows and contours have their own list of aesthetics).

dtuplot.plot_vector(nf, (x,-pi/2,3/2*pi),(y,0,2*pi),
    quiver_kw={"color":"black"},
    contour_kw={"cmap": "Blues_r", "levels": 20},
    grid=False, xlabel="x", ylabel="y",n=15)

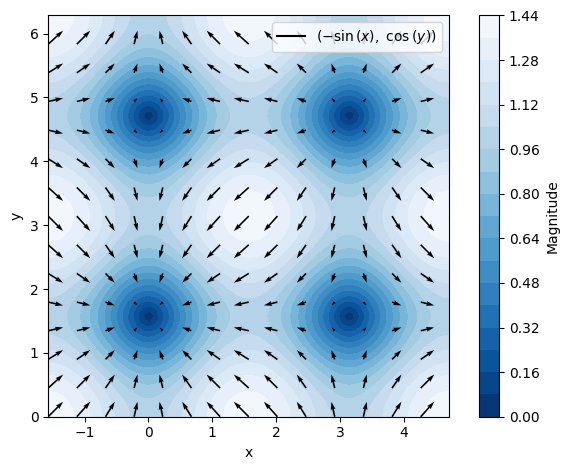
<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f1862226be0>

Which in 3D can be visualised as

p = dtuplot.plot3d(f, (x,-pi/2,3/2*pi),(y,0,2*pi),use_cm=True, camera={"elev":45, "azim":-65}, legend=True)