Welcome to Sympy!#
Sympy is the name of the program that will help in calculations and mathematics during the semesters of mathematics 1. Sympy.
Sympy is an abbreviation of “Symbolic Python”. As the name suggests, Sympy runs in the programming language Python. In Python we have the package Sympy which allows for symbolic variables and solving of symbolic equations with the programming language, which is required in the courses. We will also be introducing some other packages if necessary. Despite Python being a programming language, this is not intended as a guide in programming. We will though touch upon most if not all tools needed for solving and visualizing mathematical problems and tasks both in theoretical, applied and engineering-related use.
Sympy is imported and prepared for printing mathematics via the following two lines which will be found in the top of all following Sympy demos:
from sympy import * # We import the entire Sympy package
init_printing() # This initializes nice LaTeX output
Sympy Demo#
This document uses the format from Jupyter Notebooks. We will be showing examples of tools from Sympy that can be used for solving the weekly exercises in the Mathematics 1 courses and help solving the mathematical challenges that are introduced in the lectures of the courses. The demos will often present typical exercises and in short describe the solution methods as well as the mathematics behind them. The solutions for typical exercises will be in the form of both “simulated-manual” (solve manually with the use of Python as a calculator), native, built-in functions that solve the exercise, as well as functions that are built along the way through these demos.
Symbolic and Numerical Variables#
Python (without Sympy) is a programming language that performs computations numerically. This means that all numbers and variables must be represented by a finite number of 0’s and 1’s. The study of numerical mathematics within computers is left for other courses but it can be useful to know that Python sometimes does not act as expected due to this, unless one does something actively.
For example, we can all agree that
Even so, Python does not always agree with this
0.3-(0.2+0.1)

We do not get exactly \(0.0\), and if we ask if it is equal to \(0.0\), we get
0 == 0.3-(0.2+0.1)
False
So we have to watch out and be careful when asking whether numerical expressions are identical when using decimal numbers!
We can avoid many of such problems by letting Sympy take care of the maths! If one around either the numerator or the denominator use S(number), or use Rational(numerator, denominator), then the mathematics is handled properly by Sympy and gives the expected answer:
Rational(3,10)-(S(2)/10 + 1/S(10))

and
Rational(3,10)-(S(2)/10 + S(1)/10) == 0
True
We would also very much like to be able to solve equations. For example,
Equations like this one and much more can be solved using symbolic variables from Sympy. A Python variable can be created symbolically by use of the command Symbol() or symbols() which takes at least one argument, ‘names’. One can also provide assumptions to the variable, among others \(x\in \mathbb{Z}\) (integer=True), \(x\in \mathbb{C}\) (complex=True, this is the default if nothing is written) or \(x\in \mathbb{R}\) (complex=False or real=True).
Here we will in short give a few examples on how these variables can be used:
x = symbols('x', complex=True)
3*x**2-x
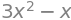
l, p, t = symbols('lambda, phi, theta', real=True)
t**2 + sin(l)/tan(p)
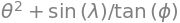
x_list = symbols('x0:3')
x_list
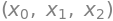
With symbolic expressions we can also solve equations with solve() or (better) solveset().
solveset(3*x**2-x)
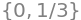
Note that \(3x^2 - x\) is an expression and not an equation one can “solve”. If solve and solveset is called with an expression, Python will solve the equation where the expressions are set equal to \(0\), meaning we are then actually solving \(3x^2-x=0\). Equations such as for example \(a=b\) can in Python be written as Eq(a,b). This is particularly useful if the right-hand side is not zero. For example:
my_equality = Eq(3*x**2-x, p+27)
my_equality

Since the equation has multiple unknowns (symbols), we have to tell with respect to which variables Python is to solve the equation:
solveset(my_equality, x)
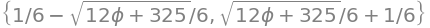
Functions and Plots#
Sympy also has a large library for both functions and plots. Here we will show briefly a few examples of this,
plot(x**2-x+3)
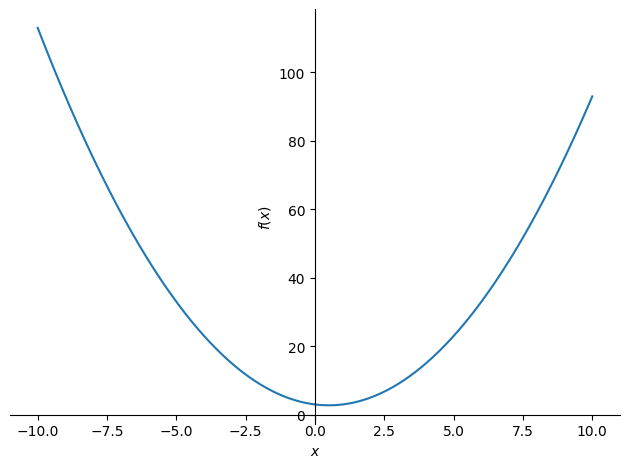
<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7f65749992b0>
Or if one wants to spend a bit more time on it so it becomes pretty:
p = plot(x+3,-x**2+3,x**2+3*x+3, (x,-2,2), show=False)
p[0].line_color = 'red'
p[1].line_color = 'green'
p[2].line_color = 'blue'
p.xlabel = "x-axis"
p.ylabel = "y-axis"
p.title = "A very nice plot"
p[0].label = '$f_0(x)=x+3$'
p[1].label = '$f_1(x)=-x^2+3$'
p[2].label = '$f_2(x)=x^2+3x+3$'
p.legend = True
p.ylim = (0,8)
p.show()
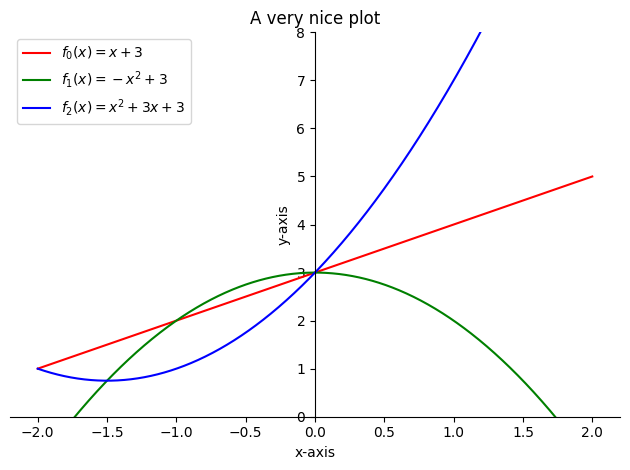
We will be covering plots much more in the upcoming demos.
Additional Notes#
Lastly, here we give a couple of extra hints for how the experience with Sympy can become easier and better.
Markdown and Code#
As already shown here there are two different modes in a Jupyter Notebook that one can write in: Markdown and Code. When focused on a Code field, you are working in Python. You can insert as many lines as you wish within a box. If you by the end in a box writes a line with a variable or an expression, this becomes printed right below with nice formatting,
y = Symbol('y', complex=True)
sqrt(y**2+2)
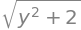
and if you in the last line write multiple things, separated by a comma, several things are printed nicely as shown here:
udtryk = sqrt(y**2+2)
udtryk, udtryk.subs({y:2/3}) <= 1.6
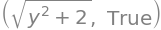
One runs a box with either Ctrl+Enter or Shift+Enter.
It is important to know that all lines that are being run are “remembered” in all boxes that are run later on. This is regardless of the order in which the boxes are run! This means that sometimes when running previous boxes, the result might not be the same as before. For example,
Welcome to Sympy!#
Sympy is the name of the program that will help in calculations and mathematics during the semesters of mathematics 1. Sympy.
Sympy is an abbreviation of “Symbolic Python”. As the name suggests, Sympy runs in the programming language Python. In Python we have the package Sympy which allows for symbolic variables and solving of symbolic equations with the programming language, which is required in the courses. We will also be introducing some other packages if necessary. Despite Python being a programming language, this is not intended as a guide in programming. We will though touch upon most if not all tools needed for solving and visualizing mathematical problems and tasks both in theoretical, applied and engineering-related use.
Sympy is imported and prepared for printing mathematics via the following two lines which will be found in the top of all following Sympy demos:
from sympy import * # We import the entire Sympy package
init_printing() # This initializes nice LaTeX output
Sympy Demo#
This document uses the format from Jupyter Notebooks. We will be showing examples of tools from Sympy that can be used for solving the weekly exercises in the Mathematics 1 courses and help solving the mathematical challenges that are introduced in the lectures of the courses. The demos will often present typical exercises and in short describe the solution methods as well as the mathematics behind them. The solutions for typical exercises will be in the form of both “simulated-manual” (solve manually with the use of Python as a calculator), native, built-in functions that solve the exercise, as well as functions that are built along the way through these demos.
Symbolic and Numerical Variables#
Python (without Sympy) is a programming language that performs computations numerically. This means that all numbers and variables must be represented by a finite number of 0’s and 1’s. The study of numerical mathematics within computers is left for other courses but it can be useful to know that Python sometimes does not act as expected due to this, unless one does something actively.
For example, we can all agree that
Even so, Python does not always agree with this
0.3-(0.2+0.1)

We do not get exactly \(0.0\), and if we ask if it is equal to \(0.0\), we get
0 == 0.3-(0.2+0.1)
False
So we have to watch out and be careful when asking whether numerical expressions are identical when using decimal numbers!
We can avoid many of such problems by letting Sympy take care of the maths! If one around either the numerator or the denominator use S(number), or use Rational(numerator, denominator), then the mathematics is handled properly by Sympy and gives the expected answer:
Rational(3,10)-(S(2)/10 + 1/S(10))

and
Rational(3,10)-(S(2)/10 + S(1)/10) == 0
True
We would also very much like to be able to solve equations. For example,
Equations like this one and much more can be solved using symbolic variables from Sympy. A Python variable can be created symbolically by use of the command Symbol() or symbols() which takes at least one argument, ‘names’. One can also provide assumptions to the variable, among others \(x\in \mathbb{Z}\) (integer=True), \(x\in \mathbb{C}\) (complex=True, this is the default if nothing is written) or \(x\in \mathbb{R}\) (complex=False or real=True).
Here we will in short give a few examples on how these variables can be used:
x = symbols('x', complex=True)
3*x**2-x
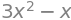
l, p, t = symbols('lambda, phi, theta', real=True)
t**2 + sin(l)/tan(p)
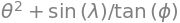
x_list = symbols('x0:3')
x_list
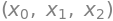
With symbolic expressions we can also solve equations with solve() or (better) solveset().
solveset(3*x**2-x)
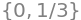
Note that \(3x^2 - x\) is an expression and not an equation one can “solve”. If solve and solveset is called with an expression, Python will solve the equation where the expressions are set equal to \(0\), meaning we are then actually solving \(3x^2-x=0\). Equations such as for example \(a=b\) can in Python be written as Eq(a,b). This is particularly useful if the right-hand side is not zero. For example:
my_equality = Eq(3*x**2-x, p+27)
my_equality

Since the equation has multiple unknowns (symbols), we have to tell with respect to which variables Python is to solve the equation:
solveset(my_equality, x)
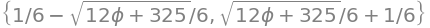
Functions and Plots#
Sympy also has a large library for both functions and plots. Here we will show briefly a few examples of this,
plot(x**2-x+3)

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7f655462b520>
Or if one wants to spend a bit more time on it so it becomes pretty:
p = plot(x+3,-x**2+3,x**2+3*x+3, (x,-2,2), show=False)
p[0].line_color = 'red'
p[1].line_color = 'green'
p[2].line_color = 'blue'
p.xlabel = "x-axis"
p.ylabel = "y-axis"
p.title = "A very nice plot"
p[0].label = '$f_0(x)=x+3$'
p[1].label = '$f_1(x)=-x^2+3$'
p[2].label = '$f_2(x)=x^2+3x+3$'
p.legend = True
p.ylim = (0,8)
p.show()

We will be covering plots much more in the upcoming demos.
Additional Notes#
Lastly, here we give a couple of extra hints for how the experience with Sympy can become easier and better.
Markdown and Code#
As already shown here there are two different modes in a Jupyter Notebook that one can write in: Markdown and Code. When focused on a Code field, you are working in Python. You can insert as many lines as you wish within a box. If you by the end in a box writes a line with a variable or an expression, this becomes printed right below with nice formatting,
y = Symbol('y', complex=True)
sqrt(y**2+2)
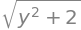
and if you in the last line write multiple things, separated by a comma, several things are printed nicely as shown here:
udtryk = sqrt(y**2+2)
udtryk, udtryk.subs({y:2/3}) <= 1.6
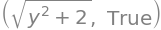
One runs a box with either Ctrl+Enter or Shift+Enter.
It is important to know that all lines that are being run are “remembered” in all boxes that are run later on. This is regardless of the order in which the boxes are run! This means that sometimes when running previous boxes, the result might not be the same as before. For example,
y ** 2
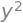
# After having run this box, try running the previous box again
y = 2
Lastly, it is worthwhile to mention that not all commands that are run in Python work if there is no solution, or if they are used wrongly. Though, sometimes this is exactly what one wants to show! For example, if a symbol cannot be transposed, an error will be displayed:
y = Symbol('y')
y.Transpose()
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
Cell In[33], line 2
1 y = Symbol('y')
----> 2 y.Transpose()
AttributeError: 'Symbol' object has no attribute 'Transpose'
If one wants to do this without seeing an error, a try/catch structure can be set up in Python:
try:
y.Transpose()
except:
print("Symbols cannot be transposed!")
Helpful Tips#
Restart: If you want Python to forget all saved variables, such as when \(y\) is given the value 2, you must restart the kernel in “main Notebook Editor toolbar” in VS Code right above the editor. “Clear Outputs of All Cells” in the same bar removes all outputs but does not cause the values of for example variables to be forgotten.
Shortcuts: If one uses Visual Studio Code, one must know about the shortcut Ctrl+Shift+P (on a Map this would be ⇧⌘P). This opens the search function for commands. If one wants to create a new cell, run the document, or create a new file, one can search for the fitting command to use. If that command will be used more in the future, one can super quickly add one’s own custom shortcut to use when needed.
Shortcuts that we have found to be extra useful while creating these demos are:
Create new boxes (insert cell below)
Change a box from Code to Markdown (change cell to code and change cell to markdown)
Restart notebook and run all boxes from the top and down (restart the kernel, then re-run the whole notebook)
Latex: In these Jupyter Notebooks there will be some examples of nice mathematics between text lines. This is LaTeX code and can be used to write nice mathematical expressions for exercises and assignments. If the mathematics is to be inline with the text, the code must be wrapped in Dollar signs $...$, and if it is to be written as an equation (centred), one can in a new line write \begin{equation} before the mathematical bit and \end{equation} after it.
Functions: Python is a large tool where only a part of it is necessary to get through courses like those for Mathematics 1. Large parts of Python can, though, make things easier if you are aware of them. An example of this is Python functions. If a series of steps is to be carried out to solve an exercise, and the same exercise repeats with different numbers, it is useful to create a function in Python. This is also supported through Sympy, and examples of this will be shown in these demos when needed. So, if a function does not already exist that can solve your problem, then you can create your own function!
Links#
These demos are made to include what is most useful during the courses, as well as which tools that are good to have in the Mathematics 1 courses. If anything is unclear or you would like to know even more about the functions, we can refer to the documentation where you can search for the functions. The three most important links are:
Basis (variables, functions and more): https://docs.sympy.org/latest/modules/core.html
Matrices: https://docs.sympy.org/latest/modules/matrices/matrices.html
Plotting: https://docs.sympy.org/latest/modules/plotting.html
Final notes#
We have tried our best to make your experience with Sympy as good as possible for your Mathematics 1 courses. But if you do find mistakes, better examples, or suggestions of improvement to these demos, we will gladly hear about it. Your feedback can be given to your TA in the course or per e-mail to s194042@student.dtu.dk or s194345@student.dtu.dk.
Good luck with Sympy and with your mathematics courses!

